Свидетельство:
О регистрации средства массовой информации: "Предотвращение аварий зданий и сооружений".
Номер: №ФС77-35253
Выдано: Федеральная служба по надзору в сфере связи и массовых коммуникаций
Дата: от 16.02.2009 г.
Форма распространения: электронное периодическое издание
Язык: русский
Учредитель: ООО "ВЕЛД"

Обрушения
электронный журнал
09.01.2016 Лерикский район, Азербайджан
Блог Шаблон
Электронный журнал
Предотвращение аварий зданий и сооружений
Новые методики определения остаточной несущей способности металлоконструкций сталеразливочных стендовПредприятие: Череповецкий государственный университет
Дата публикации: 2009-04-01
Версия для печати <<Назад

Кузьминов Александр Леонидович

Кожевников Александр Вячеславович
В процессе эксплуатации с течением времени в металлоконструкциях (МК) машин и оборудования металлургического производства происходят процессы, приводящие к снижению (потере) их работоспособности и безопасности эксплуатации. Наличие непрерывного технологического процесса при высоких температурах и силовых воздействиях, характерных для машин и оборудования металлургического производства, ускоряет эти нежелательные процессы в МК.
Основными типами повреждений являются остаточные деформации, усталостные трещины и местные деформирования элементов МК. Наиболее поврежденными являются зоны изменения сечений МК, сварные соединения, узлы крепления механизмов, концентраторы напряжений и т.д.
Характерными причинами произошедших крупных аварий являются:
- длительная эксплуатация МК при наличии усталостных трещин;
- конструкционные недостатки (высокая концентрация сварных швов, наличие концентраторов напряжений в зоне повышенной нагруженности и т.д.);
- некачественный металл и дефекты сварки;
- повышенные эксплуатационные напряжения, приводящие к превышению предела выносливости или предела текучести стали;
- воздействие высоких температур (температурные деформации, прогары и т.д.).
Своевременная оценка остаточной несущей способности и надежности МК машин и оборудования металлургического производства имеет существенное значение для обеспечения безопасной эксплуатации и ремонта в оптимальные сроки для увеличения их ресурса, а также для осуществления нормального технологического процесса.
Ключевым узлом оборудования, обеспечивающим подачу стали в сталеплавильных производствах металлургических заводов, является стенд сталеразливочных ковшей.
Сталеразливочный стенд предназначен для приема сталеразливочного ковша с жидким металлом с разливочного крана в исходном положении; передачи ковша поворотом траверсы на 180о в позицию разливки; подъема и опускания ковша для выполнения технологических операций разливки; возвращения порожнего ковша в исходную позицию. Стенд состоит из двух основных частей, подковообразных балок, предназначенных для установки сталеразливочных ковшей и траверсы, состоящей из двух балок коробчатого сечения. Траверса устанавливается на опору с помощью осей на подшипниках качения и совместно с двуплечими рычагами образует Т-образное коромысло, качательные движения которого обеспечивают подъем и опускание сталеразливочного ковша. Опора устанавливается на поворотной платформе и крепится к ней болтами. Поворотная платформа в свою очередь служит основанием поворотной части стенда. Она выполнена сварно-литой и состоит из трех частей, соединенных аналогично балкам траверсы.
Большие нагрузки (масса разливочных ковшей с расплавом 500т), непрерывный технологический процесс, температурные воздействия, ограниченность доступа к элементам и т.д. ускоряют процессы, приводящие к снижению его работоспособности и безопасности эксплуатации, а также затрудняют получение полной информации по результатам испытаний. Надежность и безопасная эксплуатация сталеразливочного стенда в первую очередь зависит от состояния его металлоконструкций, особенно после выработки нормативного срока эксплуатации.
Проблема оценки состояния несущих металлоконструкций сталеразливочных стендов актуальна не только из-за большого числа объектов, отработавших нормативный срок, но и из-за нехватки методик неразрушающего контроля для получения достоверной информации о несущей способности МК, для достоверного определения остаточного срока эксплуатации, а также отсутствием удобных для использования методик оценки надежности МК.
Предлагается новый метод испытания, который
относится к интегральному неразрушающему методу, и который можно применять
при испытании балок траверс сталеразливочных стендов. Рассмотрено два варианта
определения несущей способности МК сталеразливочных стендов: при линейной
зависимости между напряжениями и нагрузкой, а также между напряжениями и деформациями
материала, т.е. 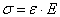 ,
, 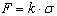 и при нелинейной зависимости
между
и при нелинейной зависимости
между  и
и 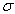 [1].
[1].
Рассмотрим методику определения несущей
способности МК сталеразливочного стенда при линейной зависимости 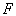 от
от 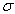 .
.
Предварительно выбирается значение испытательной нагрузки, которое может быть равно нагрузке, при которой работает сталеразливочный стенд или в 2-3 раза меньше этой нагрузки.
Суть метода в следующем. В конструкции выявляются места (элементы) с наибольшими напряжениями или усилиями от прилагаемой нагрузки, где и устанавливают измерители деформаций (перемещений). Если этого сделать не удается, то в дальнейшем необходимо произвести перерасчет по опасному сечению. Установка тензометров на балке траверсы сталеразливочного стенда (сечения 1-1 и 2-2) показана на рис. 1.
Расстановка приборов-измерителей деформаций в сечении элемента зависит от вида деформации (удлинение, укорочение, искривление, закручивание), формы и размеров поперечного сечения стержня и возможного наложения одного вида деформации на другой вид.
В двутавровых балках при равномерно распределенной или сосредоточенной нагрузке, а также в балках коробчатого сечения таким местом является верхняя или нижняя кромка (грань) балки в зависимости от формы ее поперечного сечения, как показано на рис. 2.

Рис. 1. Сечения установки измерителей деформаций
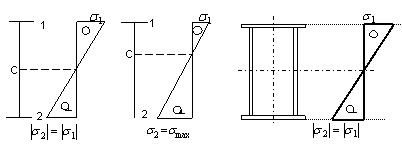
Рис. 2. Распределение напряжений в балках различных форм сечений
(с – центр тяжести сечения, индекс у 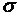 показывает место (адрес)).
Во всех
показывает место (адрес)).
Во всех
случаях в одном сечении рекомендуется устанавливать несколько измерителей
деформаций для выявления наибольшего напряжения в этом сечении
Если в ходе обследований конструкции обнаружено наличие трещин в растянутой зоне или в ходе испытаний получены подозрительно маленькие значения деформаций, то необходимо произвести установку измерителей деформаций и в сжатой зоне металлоконструкции.
В зависимости от количества нагружений (допустим 15 – 20 и более раз) возможно получение достаточной информации и, следовательно, возможная дальнейшая обработка результатов измерений по теории вероятностей и математической статистике. Но в условиях эксплуатации получить исчерпывающую статистическую информацию нередко бывает сложной, а порой и невыполнимой задачей из-за ряда существенных ограничений в условиях непрерывного производства (обеспечение технологического процесса). В этом случае дальнейшая обработка результатов измерений ведется на основе теории возможностей.
Методика определения несущей способности металлоконструкций
на основе теории вероятностей при линейной зависимости
напряжений от нагрузки
При исчерпывающей статистической информации
о величине деформации 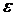 и свойствах сталей,
в частности модуля упругости стали
и свойствах сталей,
в частности модуля упругости стали 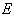 , предела текучести
, предела текучести
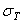 , в исследуемых сечениях
можно подобрать и проверить законы распределения случайных величин
, в исследуемых сечениях
можно подобрать и проверить законы распределения случайных величин 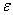 ,
, 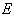 ,
, 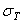 и надежно определить
параметры их распределений. В этом случае используют вероятностные методы
определения несущей способности МК.
и надежно определить
параметры их распределений. В этом случае используют вероятностные методы
определения несущей способности МК.
Вероятностный характер несущей способности МК машин и оборудования металлургического производства вызван воздействием (влиянием) целого ряда внешних и внутренних, активных и пассивных факторов. В связи с этим расчетная несущая способность, выполненная в детерминистической постановке задачи, не совпадает с действительной несущей способностью конструктивного элемента.
Рассмотрим случай, когда имеется исчерпывающая
информация об исходных данных ( 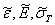 ) для нахождения предельной
нагрузки
) для нахождения предельной
нагрузки 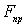 , т.е. известны законы
распределения и их параметры для случайных величин. После проведения анализа
на выброс полученных значений деформаций и других случайных величин находят
параметры распределений. Например, для нормального закона распределения это
будут среднее значение и среднее квадратическое отклонение [2].
, т.е. известны законы
распределения и их параметры для случайных величин. После проведения анализа
на выброс полученных значений деформаций и других случайных величин находят
параметры распределений. Например, для нормального закона распределения это
будут среднее значение и среднее квадратическое отклонение [2].
Известно, что статистическое математическое ожидание (среднее значение) деформации будет
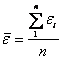 ,
,
где 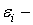 значение
значение 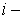 й измеренной деформации;
й измеренной деформации;
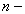 число измерений.
число измерений.
Среднее квадратическое отклонение
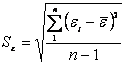 .
.
Доверительный интервал (половина ширины)
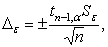
где
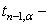 коэффициент Стьюдента,
зависящий от числа измерений
коэффициент Стьюдента,
зависящий от числа измерений 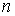 и уровня значимости
и уровня значимости
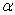 .
.
Напряжение 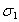 , получаемое в ходе
испытаний, определяют по закону Гука:
, получаемое в ходе
испытаний, определяют по закону Гука: 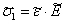 , где
, где 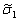 является случайной
величиной со средним значением
является случайной
величиной со средним значением  и среднеквадратическим
отклонением, найденным с использованием метода линеаризации
и среднеквадратическим
отклонением, найденным с использованием метода линеаризации
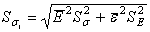 ,
,
где 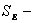 среднее квадратическое
отклонение модуля упругости. Его находят по результатам испытаний образцов.
Можно использовать зависимость
среднее квадратическое
отклонение модуля упругости. Его находят по результатам испытаний образцов.
Можно использовать зависимость 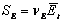 . Так как значение
. Так как значение
 коэффициент вариации,
в мировой практике принимается равным
коэффициент вариации,
в мировой практике принимается равным 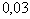 , следовательно, можно
, следовательно, можно
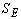 найти иначе, а именно
найти иначе, а именно
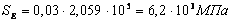 .
.
Будем считать, что 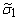 изменяется по нормальному
закону распределения. Тогда половина ширины доверительного интервала для
изменяется по нормальному
закону распределения. Тогда половина ширины доверительного интервала для
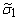
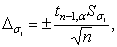
где 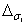 – половина ширины
доверительного интервала напряжения
– половина ширины
доверительного интервала напряжения 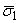 при n
числе измерений деформаций
при n
числе измерений деформаций 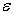 и уровне значимости
и уровне значимости
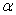 .
.
Как было отмечено, значение модуля упругости
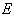 находят по результатам
испытаний образцов. Среднее значение
находят по результатам
испытаний образцов. Среднее значение 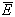 можно также принимать
по справочной или нормативной документации. В последнем случае для конструкционной
стали модуль упругости принимается
можно также принимать
по справочной или нормативной документации. В последнем случае для конструкционной
стали модуль упругости принимается 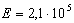 МПа. Значение коэффициента
вариации модуля упругости стали стабильно и составляет
МПа. Значение коэффициента
вариации модуля упругости стали стабильно и составляет 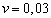 . Таким образом
. Таким образом
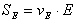 , например для стали
будем иметь
, например для стали
будем иметь 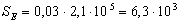 МПа.
МПа.
Обычно вырезание заготовок для испытания образцов
производится в наименее напряженных участках МК сталеразливочных стендов,
что не отражает истинного состояния физико-механических свойств металла в
самых опасных (наиболее напряженных) участках МК. Ограниченное число заготовок
диктуется требованиями «не навреди», т.е. безопасной эксплуатацией оборудования,
что сводит это количество к минимуму и, как следствие, – получение ограниченной
статистической информации, затрудняющей анализ результатов испытаний на основе
теории вероятностей и математической статистики. В этом случае значения
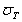 принимаются по нормативным
документам, а половину ширины доверительного интервала для
принимаются по нормативным
документам, а половину ширины доверительного интервала для 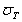 принимают равной
принимают равной
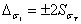 при доверительной
вероятности
при доверительной
вероятности 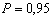 или
или 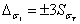 при доверительной
вероятности
при доверительной
вероятности 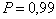 . При нормальном законе
распределения
. При нормальном законе
распределения 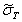 .
. 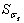 – значение среднеквадратического
отклонения предела текучести также можно найти как
– значение среднеквадратического
отклонения предела текучести также можно найти как  , где
, где  – коэффициент вариации
предела текучести. Известно, что для стали он колеблется в интервале
– коэффициент вариации
предела текучести. Известно, что для стали он колеблется в интервале
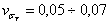 , а
, а 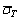 находится по нормативной
литературе. Далее строится диаграмма «нагрузка – напряжения»,
представленная на рис. 3, при линейной зависимости между нагрузкой
находится по нормативной
литературе. Далее строится диаграмма «нагрузка – напряжения»,
представленная на рис. 3, при линейной зависимости между нагрузкой 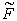 и напряжением
и напряжением
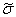 .
.

Рис. 3. Диаграмма 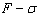 ,
, 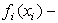 плотность вероятности
распределения
плотность вероятности
распределения 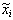
Диаграмма
строится в осях координат 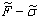 . На оси ординат откладывается
значение испытательной нагрузки
. На оси ординат откладывается
значение испытательной нагрузки 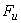 . Нагрузка будет наименьшей
(более экономичной и безопасной) при загружении конструкции в том месте, в
котором она вызовет наибольшие усилия,
например, в середине пролёта балки при изгибе. Учитывая постоянство
значения и место приложения нагрузки
. Нагрузка будет наименьшей
(более экономичной и безопасной) при загружении конструкции в том месте, в
котором она вызовет наибольшие усилия,
например, в середине пролёта балки при изгибе. Учитывая постоянство
значения и место приложения нагрузки 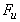 , будем считать ее
детерминированной величиной.
, будем считать ее
детерминированной величиной.
Границы доверительного
интервала 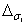 для
для 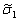 откладывают на оси
откладывают на оси
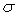 и переносят их на
прямую
и переносят их на
прямую 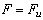 . Считая зависимость
напряжений от нагрузки линейной, через точку (
. Считая зависимость
напряжений от нагрузки линейной, через точку (
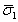 ,
, 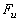 ) и начало координат
проводят прямую (луч).
) и начало координат
проводят прямую (луч).
Если необходимо
убедиться в линейной зависимости между 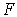 и
и 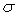 , то проводят испытания
при нескольких различных нагрузках и по найденным точкам (
, то проводят испытания
при нескольких различных нагрузках и по найденным точкам ( 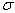 ,
, 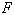 ) принимают решение
о виде зависимости между ними. Затем откладывается значение
) принимают решение
о виде зависимости между ними. Затем откладывается значение 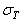 (
( 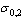 ) для стали консолей
стенда. Принимая условную диаграмму
) для стали консолей
стенда. Принимая условную диаграмму 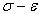 , по Прандтлю находят
точку пересечения луча в осях координат
, по Прандтлю находят
точку пересечения луча в осях координат 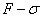 с прямой (или
с прямой (или
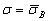 ). Откладывают от нее
значение
). Откладывают от нее
значение  параллельно оси
параллельно оси
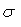 и проводят доверительные
границы
и проводят доверительные
границы 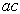 и
и 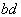 , как показано на рис.
3. Из левой точки b доверительного интервала
, как показано на рис.
3. Из левой точки b доверительного интервала
 опускают вертикаль
до нижней доверительной границы и через полученную точку пересечения проводят
горизонталь до пересечения с осью
опускают вертикаль
до нижней доверительной границы и через полученную точку пересечения проводят
горизонталь до пересечения с осью 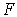 .
.
Полученная
точка на оси ординат укажет нижнее значение предельной нагрузки 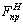 , пересечение
с верхней доверительной границей – верхнее значение придельной нагрузки
, пересечение
с верхней доверительной границей – верхнее значение придельной нагрузки
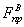 .
.
Из диаграммы 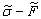 видно,
что предельная нагрузка
видно,
что предельная нагрузка 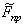 является случайной
величиной, так как зависит от случайных
является случайной
величиной, так как зависит от случайных 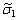 и
и 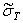 .
.
Представим эту зависимость в аналитической форме, в виде линейной зависимости
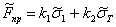 ,
,
которую, согласно диаграмме
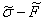 , можно представить
в виде системы уравнений
, можно представить
в виде системы уравнений
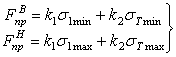 ,
,
где 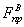 ;
; 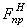 – соответственно верхнее
и нижнее значения предельной нагрузки, определенные по диаграмме
– соответственно верхнее
и нижнее значения предельной нагрузки, определенные по диаграмме
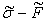 .
.
Решая систему уравнений, находим постоянные
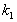 и
и  .
.
На их основе находим значение предельной нагрузки
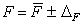 при определенном уровне
значимости
при определенном уровне
значимости 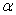 , где
, где 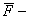 среднее значение предельной
нагрузки
среднее значение предельной
нагрузки 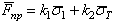 ;
; 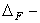 половина ширины
доверительного интервала
половина ширины
доверительного интервала  ;
; 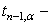 коэффициент Стьюдента,
зависящий от числа измерений
коэффициент Стьюдента,
зависящий от числа измерений 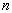 и уровня значимости
и уровня значимости
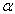 ;
; 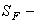 среднеквадратическое
отклонение предельной нагрузки
среднеквадратическое
отклонение предельной нагрузки 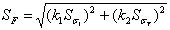 , где
, где 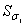 и
и  среднеквадратические
отклонения экспериментального напряжения и предела текучести.
среднеквадратические
отклонения экспериментального напряжения и предела текучести.
Методика определения несущей способности
металлоконструкций при нелинейной зависимости
Предлагаемый метод отличается от описанного ранее
тем, что диаграмма 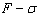 будет криволинейной,
которую можно аппроксимировать полиномом nй степени
будет криволинейной,
которую можно аппроксимировать полиномом nй степени
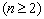 . В связи с этим испытания
балки траверсы проводятся, как минимум, тремя разными по величине нагрузками,
каждая последующая испытательная нагрузка больше предыдущей, т.е. должно выполняться
условие
. В связи с этим испытания
балки траверсы проводятся, как минимум, тремя разными по величине нагрузками,
каждая последующая испытательная нагрузка больше предыдущей, т.е. должно выполняться
условие 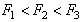 . Последняя испытательная
нагрузка, в данном случае
. Последняя испытательная
нагрузка, в данном случае 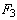 , может быть меньше
или равной той нагрузке, при которой эксплуатируется сталеразливочный стенд.
, может быть меньше
или равной той нагрузке, при которой эксплуатируется сталеразливочный стенд.
Затем, после каждого нагружения балки траверсы
сталеразливочного стенда нагрузкой 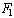 измеряется деформация
измеряется деформация
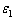 несколько раз. Аналогично
поступают при нагружениях конструкции нагрузками
несколько раз. Аналогично
поступают при нагружениях конструкции нагрузками 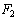 и
и 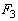 .
.
По полученным значениям средних деформаций
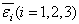 и нагрузкам
и нагрузкам
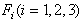 строится диаграмма
строится диаграмма
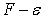 , и доверительные границы
, и доверительные границы
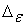 , как показано на
рис. 4. Значение предельной деформации
, как показано на
рис. 4. Значение предельной деформации 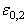 , соответствующее условному
пределу текучести
, соответствующее условному
пределу текучести 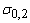 , принимается из нормативной
литературы. В частности диаграмма аппроксимируется полиномом второй степени
, принимается из нормативной
литературы. В частности диаграмма аппроксимируется полиномом второй степени
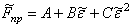 . Применяя метод наименьших
квадратов, получим систему уравнений для нахождения коэффициентов
. Применяя метод наименьших
квадратов, получим систему уравнений для нахождения коэффициентов 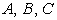 .
.
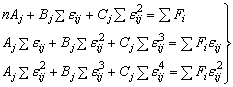 ,
,
где  – номер опыта (испытания),
в нашем примере
– номер опыта (испытания),
в нашем примере 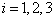 (см. рис. 4);
(см. рис. 4);
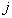 – номер кривой, число
которых в нашем примере равно трем (
– номер кривой, число
которых в нашем примере равно трем ( 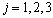 );
);
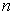 – число испытаний
или число пар
– число испытаний
или число пар 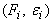 .
.
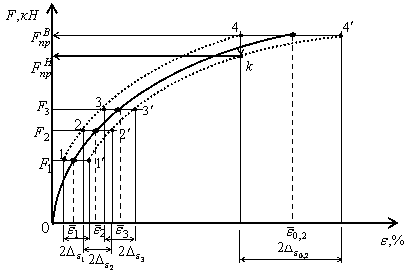
Рис. 4. Диаграмма 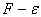 при неизвестном
при неизвестном
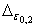
Такие же кривые строят по точкам доверительных
интервалов в виде доверительных границ. Если же 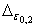 известно по результатам
испытания образцов, изготовленных из заготовок испытываемой МК, то в этом
случае имеем две экспериментально полученные дополнительные точки
известно по результатам
испытания образцов, изготовленных из заготовок испытываемой МК, то в этом
случае имеем две экспериментально полученные дополнительные точки 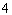 и
и 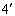 , как показано на рис.
5.
, как показано на рис.
5.
В связи с тем, что результатов испытаний, как
показала практика наших испытаний, мало (3-4 при каждом 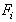 ), то анализ неопределенностей
осуществляется методами теории возможностей. По этой теории среднее значение
деформации при одном значении
), то анализ неопределенностей
осуществляется методами теории возможностей. По этой теории среднее значение
деформации при одном значении 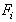 находится по условию
находится по условию
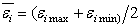 ,
, 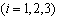 , а доверительный интервал
, а доверительный интервал
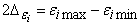 ,
,  и
и 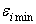 – граничные значения
доверительного интервала. Для полиномов более высокой степени число испытательных
нагрузок
– граничные значения
доверительного интервала. Для полиномов более высокой степени число испытательных
нагрузок 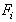 и число испытаний
соответственно увеличивают.
и число испытаний
соответственно увеличивают.
Нахождение значений 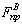 и
и 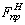 осуществляется по
построенным диаграммам
осуществляется по
построенным диаграммам  геометрически, как
показано на рис. 4 или рис. 5.
геометрически, как
показано на рис. 4 или рис. 5.
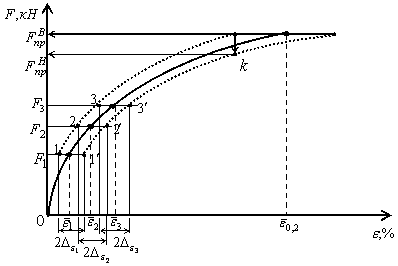
Рис. 5. Диаграмма 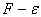 при известном
при известном
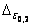
Предполагаем, что 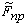 изменяется по равномерному
закону распределения с известными
изменяется по равномерному
закону распределения с известными 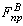 и
и 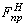 , как показано на рис.
6. Известно, что с точки зрения теории вероятностей в условиях полной неопределенности
гипотеза о равномерном распределении вероятности измеряемой величины на некотором
интервале ее значения является универсальным способом учета дефицита информации.
В данном случае рассматривается интервал
, как показано на рис.
6. Известно, что с точки зрения теории вероятностей в условиях полной неопределенности
гипотеза о равномерном распределении вероятности измеряемой величины на некотором
интервале ее значения является универсальным способом учета дефицита информации.
В данном случае рассматривается интервал  .
.
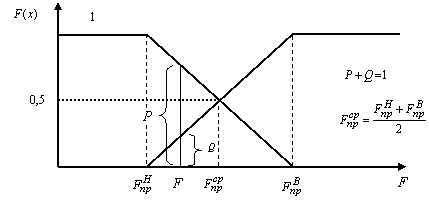
Рис. 6. Равномерный закон распределения
Рассматривается вероятность того, что эксплуатационная
нагрузка 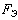 меньше предельной
меньше предельной
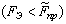 .
.
При 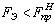 вероятность безотказной
работы
вероятность безотказной
работы 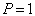 , а вероятность отказа
, а вероятность отказа
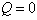 .
.
При 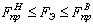 вероятность безотказной
работы
вероятность безотказной
работы 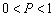 , а вероятность отказа
, а вероятность отказа
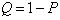 .
.
При 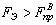 вероятность безотказной
работы
вероятность безотказной
работы 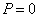 , а вероятность отказа
, а вероятность отказа
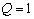 .
.
Таким образом, проблема оценки технического состояния несущих МК сталеразливочных стендов актуальна из-за большого числа объектов, отработавших нормативный срок, и из-за отсутствия методик неразрушающего контроля для получения достоверной информации о несущей способности МК, по оценке надежности МК и достоверного определения остаточного ресурса.
Разработка и применение методов, позволяющих определять несущую способность, надежность и ресурс МК сталеразливочных стендов машин непрерывного литья заготовок металлургического производства, экономически целесообразны и необходимы по условию безопасности производства и возможности выявления резерва несущей способности.
Библиографический список
- Прогнозирование долговечности материалов и конструктивных элементов при ограниченной статистической информации / В.С.Уткин, Д.А. Погодин // Конструкции из композиционных материалов. – 2003. - №1. - С.71-74.
- Математическое моделирование при расчетах и исследованиях строительных конструкций. Учеб. пособие / В.В. Горев, В.В.Филипов, Н.Ю.Тезиков. – М.: Высшая школа, 2002. – 206 с.




