Свидетельство:
О регистрации средства массовой информации: "Предотвращение аварий зданий и сооружений".
Номер: №ФС77-35253
Выдано: Федеральная служба по надзору в сфере связи и массовых коммуникаций
Дата: от 16.02.2009 г.
Форма распространения: электронное периодическое издание
Язык: русский
Учредитель: ООО "ВЕЛД"

Обрушения
электронный журнал
09.01.2016 Лерикский район, Азербайджан
Блог Шаблон
Электронный журнал
Предотвращение аварий зданий и сооружений
О критериях живучести железобетонных коррозионно повреждаемых конструктивных систем в запредельных состоянияхПредприятие: Орловский государственный технический университет
Дата публикации: 2009-04-01
Версия для печати <<Назад

Клюева Наталия Витальевна

Андросова Наталия Борисовна
Рассматриваются элементы новой концепции создания и эксплуатации зданий и сооружений. В ее основу положена современная модель защиты объектов недвижимости, базирующаяся на понятиях конструктивной безопасности зданий и сооружений как характеристики неразрушимости в течение расчётного эксплуатационного периода и живучести как характеристики неразрушимости при запредельных внешних воздействиях в течение расчётного эвакуационного промежутка времени. В качестве фрагмента разрабатываемой теории приводится решение задачи о критериях живучести железобетонных коррозионно повреждаемых конструктивных систем в запредельных состояниях.
Внезапные изменения структуры конструкции при запроектных воздействиях являются одним из основных факторов, определяющих не только картину ее напряженно-деформированного состояния и характер выключения связей и отдельных элементов, но и картину разрушения конструктивной системы в целом. Иными словами по характеру структурных изменений можно оценивать степень конструктивной нелинейности системы и, как следствие, ее живучесть.
В настоящей статье приведены некоторые результаты исследования по формированию критериев живучести железобетонных балочных и рамных конструкций от воздействий, вызывающих внезапные структурные изменения в этих конструкциях.
В работах [1; 2] были представлены расчетные зависимости для оценки живучести рамно-стержневых конструктивных систем при внезапных структурных изменениях в таких системах от накопления в них коррозионных повреждений. Квазистатический расчет рассматриваемых конструкций выполнен с использованием неординарного смешанного метода расчета статически неопределимых систем.
Особенностью рассматриваемого варианта смешанного
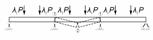
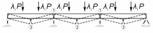
метода является то, что основная система неразрезной балки (рис. 1) или рамы
(рис. 2) выбирается в виде шарнирного полигона с удаленными в местах возможного
выключения связями и заменой их неизвестными 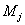 (
( 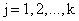 ). Если при удалении
связей образуется геометрически изменяемая основная система, то накладываются
дополнительные связи
). Если при удалении
связей образуется геометрически изменяемая основная система, то накладываются
дополнительные связи 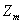 (
( 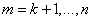 ).
).
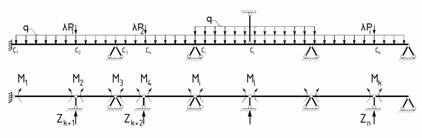
Рис. 1. Заданная (а) и основная (б) системы смешанного
метода
при расчете неразрезных балок
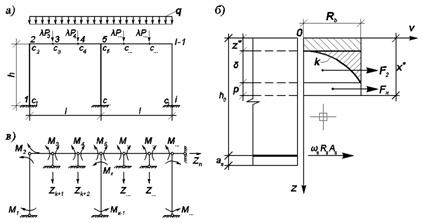
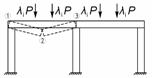
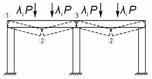
Рис. 2. Заданная (а), основная (в) системы рамы и расчетная
схема
поперечного сечения железобетонного элемента (б)
Пусть при значении параметра нагрузки 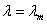 в системе
выключится i-ая связь. Выключение связи произойдет
в том случае, когда усилие в ней достигнет предельного значения. На рис. 2,а
эти сечения обозначены соответственно
в системе
выключится i-ая связь. Выключение связи произойдет
в том случае, когда усилие в ней достигнет предельного значения. На рис. 2,а
эти сечения обозначены соответственно 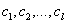 . Найти значение параметра
. Найти значение параметра
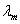 можно,
используя канонические уравнения смешанного метода:
можно,
используя канонические уравнения смешанного метода:
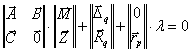 ,
(1)
,
(1)
где 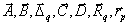 – матрицы
коэффициентов неизвестных
– матрицы
коэффициентов неизвестных 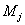 и
и
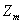 смешанного
метода.
смешанного
метода.
В развернутом виде система уравнений (1) имеет вид:
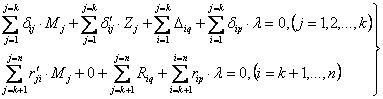 , (2)
, (2)
где 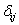 ,
, 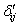 ,
, 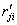 – коэффициенты
при неизвестных (единичные перемещения и реакции) смешанного метода расчета
статически неопределимых систем;
– коэффициенты
при неизвестных (единичные перемещения и реакции) смешанного метода расчета
статически неопределимых систем;
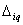 и
и
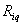 – грузовые коэффициенты
(перемещение и реакции соответственно) от постоянной нагрузки;
– грузовые коэффициенты
(перемещение и реакции соответственно) от постоянной нагрузки;
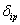 – перемещение
по направлению i-ой удаленной связи от внешней параметрической нагрузки
при λ=1;
– перемещение
по направлению i-ой удаленной связи от внешней параметрической нагрузки
при λ=1;
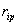 – реакция
в i-ой наложенной связи основной системы от внешней параметрической
нагрузки при λ=1.
– реакция
в i-ой наложенной связи основной системы от внешней параметрической
нагрузки при λ=1.
За критерий живучести системы принимается
величина действующей на нее нагрузки, равная величине нагрузки, при которой
рассматриваемая система переходит в изменяемую систему (без лишних связей).
Для превращения n-раз статически неопределимой системы в геометрически изменяемую
систему необходимо исключить из нее не менее (n+1)
связей. Методами строительной механики определяется величина нагрузки, которая
вызывает изменяемость системы. При внезапном приложении запроектной нагрузки
в условиях чрезвычайных ситуаций природного или техногенного характера в конструктивной
системе возникают динамические догружения и при расчете к величине статической
нагрузки должна добавляться динамическая составляющая. На начальном этапе
часть нагрузки 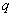 , при действии которой
не происходит выключения связей (например, собственный вес), считается постоянной.
Остальная часть – переменная нагрузка или коррозионное повреждение, изменяется
пропорционально одному параметру
, при действии которой
не происходит выключения связей (например, собственный вес), считается постоянной.
Остальная часть – переменная нагрузка или коррозионное повреждение, изменяется
пропорционально одному параметру 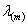 , т.е. параметрически.
Причем изменение переменной нагрузки происходит пропорционально этому параметру.
, т.е. параметрически.
Причем изменение переменной нагрузки происходит пропорционально этому параметру.
Таким образом, в данном случае постановка задачи
расчета рамы на первом этапе сводится к определению предельной величины параметра
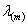 , при котором в раме
образуется m-й шарнир, нагруженный статической
нагрузкой, в условиях внезапного аварийного динамического догружения [3; 4].
, при котором в раме
образуется m-й шарнир, нагруженный статической
нагрузкой, в условиях внезапного аварийного динамического догружения [3; 4].
Формализация представленного критерия живучести рассматриваемых конструктивных систем может быть выполнена решением системы уравнений (1):
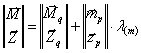 .
(3)
.
(3)
Для принятой двучленной формы записи грузовых коэффициентов, значения усилий в выключающихся связях от суммарного воздействия заданной и параметрической нагрузок определяются по формуле
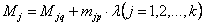 ,
(4)
,
(4)
где 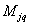 и
и
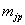 – соответственно
j-е элементы матриц-столбов
– соответственно
j-е элементы матриц-столбов 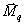 и
и
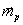 .
.
Выключение связи произойдет в том случае, когда усилие в ней достигнет предельного значения. Тогда для всех усилий в выключающихся связях должна удовлетворяться система неравенств:
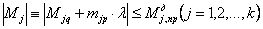 ,
(5)
,
(5)
где 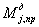 – предельное
значение динамического момента в j-й связи определенное по значению ресурса силового сопротивления
сечения элемента с учетом динамической прочности бетона сжатой зоны.
– предельное
значение динамического момента в j-й связи определенное по значению ресурса силового сопротивления
сечения элемента с учетом динамической прочности бетона сжатой зоны.
Ресурс силового сопротивления, например, для изгибаемого элемента по нормальному сечению (рис. 2,б), оцениваемый по предельному усилию в сжатом бетоне, для поврежденного коррозией бетона определяется из выражения [3]:
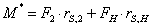 ,
(6)
,
(6)
где 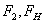 и
и
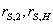 – действующие
в переходной и неповрежденной областях сжатого бетона силы и соответствующие
им моментные плечи относительно центра тяжести растянутой арматуры, выраженные
как функции толщины поврежденной, частично поврежденной и неповрежденной областей
сжатого бетона высотой
– действующие
в переходной и неповрежденной областях сжатого бетона силы и соответствующие
им моментные плечи относительно центра тяжести растянутой арматуры, выраженные
как функции толщины поврежденной, частично поврежденной и неповрежденной областей
сжатого бетона высотой 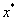 .
.
Используя предложенную профессором В.М. Бондаренко слоистую расчетную модель сжатого бетона для поврежденного коррозией железобетонного элемента, значение предельной глубины повреждения может быть определено с помощью так называемой функции повреждений, которая записывается в форме полинома:
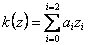 .
(7)
.
(7)
Из геометрических условий (см. рис. 2,б) находим:
-
при 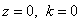 ;
;
-
при 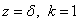 и
и
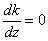 .
.
Отсюда находим значение коэффициента 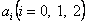 :
:
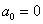 ;
; 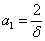 ;
; 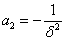 .
(8)
.
(8)
Поскольку 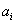 при
при
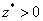 находится
только из геометрических условий, то функция повреждений k
остается единой для всех характеристик силового сопротивления поврежденного
бетона: прочности, модуля мгновенной деформации, ползучести и т.п.
находится
только из геометрических условий, то функция повреждений k
остается единой для всех характеристик силового сопротивления поврежденного
бетона: прочности, модуля мгновенной деформации, ползучести и т.п.
Численная реализация представленного критерия живучести (λm) железобетонных рамно-стержневых систем выполнена применительно к конструкциям неразрезных балочных и рамных систем, экспериментальные исследования которых выполнены ранее Г.А. Гениевым, Н.В. Клюевой, А.И. Демьяновым [5; 6], О.А. Ветровой, Е.А. Скобелевой [7; 8]. Результаты расчетов по определению параметра живучести λm опытной и расчетной схем разрушения для рассматриваемых конструктивных систем приведены в таблице.
Расчетные схемы разрушения конструктивных
систем
и значения критерия живучести λm
| № п/п |
Шифр опытной конструкции |
Схема разрушения и последовательность образования пластических шарниров (или швов сдвига) |
Значение λm при |
Характер разрушения конструктивной схемы |
||
| i=1 |
i=2 |
i=3 |
||||
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 1 |
ОБ – I |
|
4,39 |
7,37 |
– |
Хрупкое по бетону во |
| 2 |
ОБ-II |
|
2,59 |
4,35 |
4,35 |
То же в 1-м, 2-м и 3-м пролетах |
| 3 |
ОБС - I |
|
6,29 |
10,5 |
– |
По шву сдвига в 1-м пролете, затем по норм. сечению во 2-м пролете |
| 4 |
ОБС-II |
|
5,76 |
9,84 |
9,84 |
То же в 1-м, 2-м и 3-м пролетах |
| 5 |
Р-I |
|
4,09 |
7,14 |
8,01 |
Хрупкое разрушение ригеля по бетону в 1-м пролете |
| 6 |
Р-II |
|
3,6 |
6,28 |
7,04 |
То же в 1-м и 2-м пролетах |
| 7 |
ОР-I |
|
4,05 |
6,93 |
7,76 |
Разрушение ригеля по шву сдвига, а затем по нормальному сечению в 1-м пролете |
| 8 |
ОР-II |
|
4,05 |
6,96 |
7,79 |
То же в 1-м и 2-м пролетах |
Проиллюстрируем расчет критерия живучести λm на примере разрушения опытной конструкции ОБ-I (рис. 3,а,б).
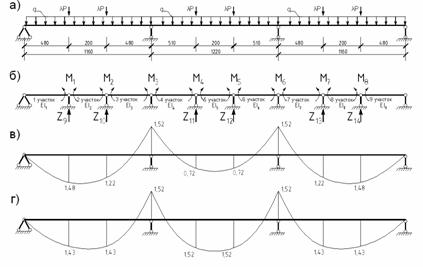
Рис. 3. Расчетная схема 3-пролетной балки (а), основная
система смешанного
метода (б), эпюры моментов при
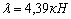 (в) и
(в) и 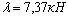 (г)
(г)
Опытная конструкция трехпролетной неразрезной балки была рассчитана и заармирована таким образом, чтобы при загружении всех ее пролетов проектной нагрузкой в виде распределенной (собственный вес), сосредоточенных сил и при внезапном выключении моментной связи над первой промежуточной опорой произошло локальное разрушение только одного пролета балочной системы. Сечение балки принято сплошное с размерами 120×40мм, бетон класса В25. Армирование плоскими сварными каркасами: продольная рабочая нижняя арматура диаметром 8мм, продольная верхняя арматура диаметром 6мм; поперечная арматура – проволока диаметром 1,5мм с шагом 60мм.
Решение
1. На основе феноменологической модели развития повреждений железобетона [3] остаточный ресурс силового сопротивления по нормальному сечению определяется следующим образом (рис. 4).
Если принять, что область разрушенного бетона
занимает всю высоту 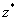 , то высота поврежденной
сжатой зоны бетона в соответствии с [3] будет равна:
, то высота поврежденной
сжатой зоны бетона в соответствии с [3] будет равна:
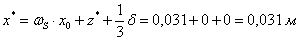 ,
,
где 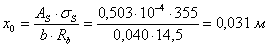 – высота
сжатой зоны неповрежденного бетона (
– высота
сжатой зоны неповрежденного бетона ( 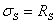 при условии
при условии
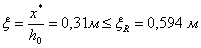 );
);
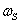 – коэффициент
коррозионного повреждения рабочей арматуры (в данном расчете условно принят
1).
– коэффициент
коррозионного повреждения рабочей арматуры (в данном расчете условно принят
1).
Остаточный ресурс силового сопротивления сечения определяем по формуле (6):
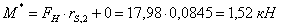 ,
,
где 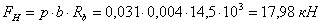 ;
;
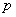 – высота
неразрушенной области сжатого бетона, в рассматриваемом примере
– высота
неразрушенной области сжатого бетона, в рассматриваемом примере 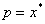 (см. рис. 4);
(см. рис. 4);
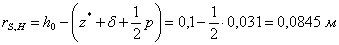 .
.
Остаточный ресурс силового сопротивления элементов
балочной системы для всех трех образцов балок: ОБ-I-1;
ОБ-I-2; ОБ-I-3 – 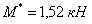 . Изгибная жесткость
балок, работающих в стадии с трещинами, вычисляется по методике [8], при
. Изгибная жесткость
балок, работающих в стадии с трещинами, вычисляется по методике [8], при
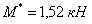 составила
составила
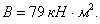
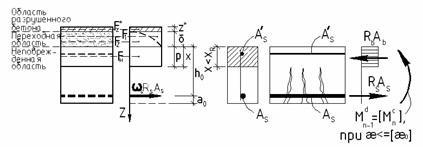
Рис. 4. Схема расчетной модели сечения железобетонного
элемента балки
в запредельном состоянии при пластическом «мягком» случае разрушения
2. Формируем систему линейных алгебраических уравнений смешанного метода (2) для решаемой задачи:
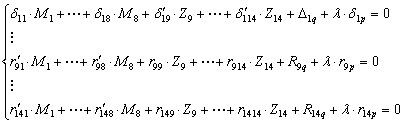
Например, матрица 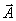 имеет
вид:
имеет
вид:
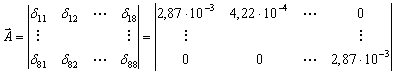 .
.
Из множества решений системы неравенств (5) определяем
минимальное значение 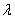 , при котором в наиболее
нагруженной выключающейся связи достигается предельное значение, т.е. произойдет
ее выключение:
, при котором в наиболее
нагруженной выключающейся связи достигается предельное значение, т.е. произойдет
ее выключение: 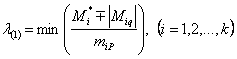 .
.
Решая систему неравенств, получим, что первым
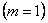 образуется
шарнир в сечениях 3 и 6 (рис. 3,в):
образуется
шарнир в сечениях 3 и 6 (рис. 3,в):
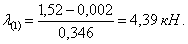
Аналогичным образом получаем, что образуются
шарниры 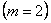 в сечениях 4 и 5 (рис. 3,г):
в сечениях 4 и 5 (рис. 3,г):
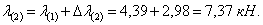
На следующем этапе нагружения определитель матрицы системы (2) обращается в ноль – признак окончания расчета.
Библиографический список
- Гениев Г.А. Прочность и деформативность железобетонных конструкций при запроектных воздействиях/ Г.А. Гениев, В.И. Колчунов, Н.В. Клюева, А.И. Никулин, К.П. Пятикрестовский. Научное издание. – М.: Изд-во АСВ, 2004. – 216 с.
- Клюева Н.В. Расчет живучести коррозионно повреждаемых железобетонных рам с односторонними связями / Н.В. Клюева // Бетон и железобетон. – 2008. – №2. – С. 19-21.
- Бондаренко В.М. К расчету сооружений, меняющих расчетную схему вследствие коррозионных повреждений / В.М. Бондаренко, Н.В. Клюева // Известия вузов. Серия «Строительство». – 2008. – №1. –С. 4-12.
- Бондаренко В.М. Оптимизация живучести конструктивно нелинейных железобетонных рамно-стержневых систем при внезапных структурных изменениях / В.М. Бондаренко, Н.В Клюева, А.Н. Дегтярь, Н.Б. Андросова // Известия ОрелГТУ. Серия «Строительство. Транспорт». - №4, 2007. – С.5-10.
- Гениев Г.А. Экспериментально-теоретические исследования неразрезных балок при аварийном выключении из работы отдельных элементов / Г.А. Гениев, Н.В. Клюева// Известия ВУЗов. Строительство. – 2000. – №10. – С.21-26.
- Клюева. Н.В Экспериментальные исследования железобетонных балок сплошного и составного сечения в запредельных состояниях /. Н.В. Клюева, А.И. Демьянов // VII Международный научно-методический семинар «Перспективы развития новых технологий в строительстве и подготовке инженерных кадров Республики Беларусь». – Брест. –2001. – С. 167-172.
- Ветрова, О.А. Экспериментальные исследования рамно-стержневых железобетонных конструкций в запредельных состояниях [ /О.А. Ветрова, Н.В. Клюева// Изв. Орел ГТУ. Серия «Строительство. Транспорт». – Орел: Орел ГТУ. – 2005. – №3-4. – С. 10-15.
- Колчунов Вл.И. Экспериментальные исследования деформативности и трещиностойкости железобетонных конструкций составного сечения / Вл.И. Колчунов, Е.А. Скобелева, Н.В. Клюева, С.И. Горностаев// Строительная механика инженерных конструкций и сооружений. – 2008. – №1. – С.54-60.